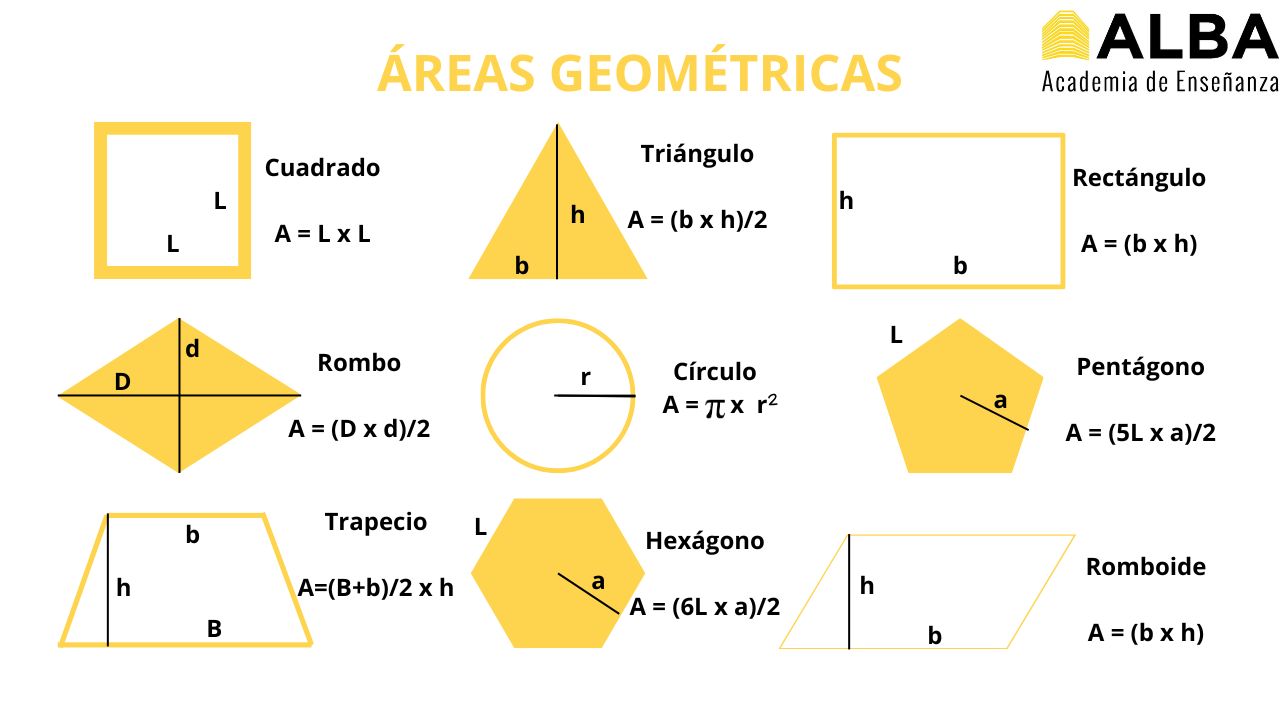
Calcular el área de las figuras geométricas es esencial en matemáticas y tiene múltiples aplicaciones prácticas en la vida cotidiana, desde la planificación de espacios hasta la construcción y el diseño. A continuación, te explicaremos detalladamente cómo determinar el área de diversas figuras geométricas, proporcionando las fórmulas correspondientes y explicando cada uno de sus parámetros.
El área es la medida de la superficie encerrada dentro de una figura geométrica. Se expresa en unidades cuadradas, como centímetros cuadrados (cm²) o metros cuadrados (m²), y representa el espacio bidimensional que ocupa la figura. Por ejemplo, el área de un cuadrado de 3 cm de lado es 9 cm², ya que cubre una superficie de 9 cuadrados de 1 cm² cada uno.
Es común confundir el área con el perímetro, pero son conceptos distintos:
Por ejemplo, en un rectángulo de 4 cm de ancho y 6 cm de largo:
Comprender esta diferencia es fundamental para resolver problemas geométricos correctamente.
Un cuadrado es un polígono de cuatro lados iguales y ángulos rectos (90°). La fórmula para calcular su área es:
Fórmula:
Donde:
Ejemplo:
Si un cuadrado tiene un lado de 5 cm:
Por lo tanto, el área del cuadrado es 25 cm².
Un rectángulo es un polígono de cuatro lados donde los lados opuestos son iguales y todos sus ángulos son rectos. La fórmula para calcular su área es:
Fórmula:
Donde:
Ejemplo:
Si un rectángulo tiene una base de 8 cm y una altura de 3 cm:
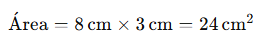
Por lo tanto, el área del rectángulo es 24 cm².
Un triángulo es un polígono de tres lados. La fórmula general para calcular su área es:
Fórmula:
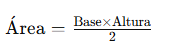
Donde:
Ejemplo:
Si un triángulo tiene una base de 10 cm y una altura de 5 cm:
Por lo tanto, el área del triángulo es 25 cm².
Un círculo es una figura geométrica plana formada por todos los puntos que están a una distancia fija (radio) de un punto central. La fórmula para calcular su área es:
Fórmula:
Donde:
Ejemplo:
Si un círculo tiene un radio de 7 cm:
Por lo tanto, el área del círculo es 153,94 cm² (redondeando a dos decimales).
El romboide (también conocido como paralelogramo) es una figura de cuatro lados con lados opuestos paralelos e iguales, pero no necesariamente con ángulos rectos.
Fórmula:
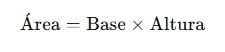
Donde:
Ejemplo:
Si un romboide tiene una base de 6 cm y una altura de 4 cm:
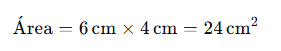
Un trapecio es un cuadrilátero que tiene dos lados paralelos (bases) y dos no paralelos.
Fórmula:
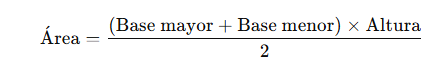
Donde:
Ejemplo:
Si un trapecio tiene una base mayor de 10 cm, una base menor de 6 cm y una altura de 4 cm:
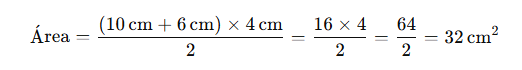
Por lo tanto, el área del trapecio es 32 cm².
El rombo es un cuadrilátero con los cuatro lados iguales y con diagonales que se cruzan en ángulo recto.
Fórmula:
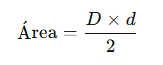
Donde:
Ejemplo:
Si un rombo tiene una diagonal mayor de 10 cm y una menor de 6 cm:
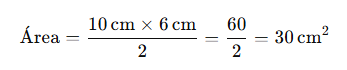
Por lo tanto, el área del rombo es 30 cm².
Un pentágono es un polígono de cinco lados. Si es regular (todos sus lados y ángulos son iguales), se puede calcular su área mediante la siguiente fórmula:
Fórmula:
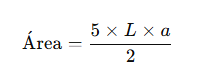
Donde:
Ejemplo:
Si un pentágono tiene lados de 6 cm y una apotema de 4.1 cm:
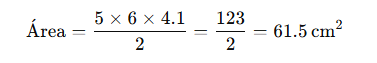
El área del pentágono es 61,5 cm².
Un hexágono es un polígono de seis lados. Si es regular, podemos calcular su área con esta fórmula:
Fórmula:
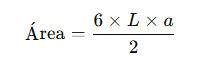
Donde:
Ejemplo:
Si un hexágono tiene lados de 5 cm y una apotema de 4.3 cm:
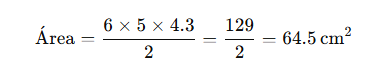
Por tanto, el área del hexágono es 64,5 cm².
Este contenido está orientado a estudiantes de la ESO y Bachillerato que deseen aprender a calcular áreas con claridad y precisión. En Academia Murcia, te ayudamos a comprender y dominar estos conceptos con clases personalizadas, material adaptado a tu nivel y un equipo de profesores especializados en matemáticas. ¡Contáctanos y prepárate con los mejores!
| Cookie | Duración | Descripción |
|---|---|---|
| cookielawinfo-checkbox-analytics | 11 months | This cookie is set by GDPR Cookie Consent plugin. The cookie is used to store the user consent for the cookies in the category "Analytics". |
| cookielawinfo-checkbox-functional | 11 months | The cookie is set by GDPR cookie consent to record the user consent for the cookies in the category "Functional". |
| cookielawinfo-checkbox-necessary | 11 months | This cookie is set by GDPR Cookie Consent plugin. The cookies is used to store the user consent for the cookies in the category "Necessary". |
| cookielawinfo-checkbox-others | 11 months | This cookie is set by GDPR Cookie Consent plugin. The cookie is used to store the user consent for the cookies in the category "Other. |
| cookielawinfo-checkbox-performance | 11 months | This cookie is set by GDPR Cookie Consent plugin. The cookie is used to store the user consent for the cookies in the category "Performance". |
| viewed_cookie_policy | 11 months | The cookie is set by the GDPR Cookie Consent plugin and is used to store whether or not user has consented to the use of cookies. It does not store any personal data. |
| Cookie | Duración | Descripción |
|---|---|---|
| _ga | 2 years | The _ga cookie, installed by Google Analytics, calculates visitor, session and campaign data and also keeps track of site usage for the site's analytics report. The cookie stores information anonymously and assigns a randomly generated number to recognize unique visitors. |
| _ga_8LZX9ZTH59 | 2 years | This cookie is installed by Google Analytics. |
| _gat_gtag_UA_190442266_1 | 1 minute | Set by Google to distinguish users. |
| _gid | 1 day | Installed by Google Analytics, _gid cookie stores information on how visitors use a website, while also creating an analytics report of the website's performance. Some of the data that are collected include the number of visitors, their source, and the pages they visit anonymously. |